归一化（Normalization）

目的：

应用层面需要统一量纲
在使用梯度下降发求解最优化问题时，归一化或标准化后可以加快梯度下降的求解速度，即提升收敛速度
可以避免神经元饱和。神经元的激活在0或1时会饱和，这些区域梯度几乎为0，这样的话在反向传播的时候局部梯度也会接近0。因此归一化可以有效缓解梯度消失
避免数据中小的数值被大数值吞噬，也避免数值太大引发的数值问题。（输入图像的值）

为什么要归一化

假设w1在[-10,10],w2在[-100,100]，梯度每次都前进一个单位，则w1在搜索全局最优时会相对来说走的更『快』。即提高了收敛速度

归一化类型

线性归一化

$x^{'}=\frac{x-min(x)}{max(x)-min(x)}$

标准归一化

$x^{'}=\frac{x-\mu}{\sigma}$

归一化后均值为0，标准差为1，$ \mu $ 为左右样本数据的均值，$\sigma$ 是所有样本数据的标准差。

批归一化（Batch Normalization）

在网络中间对数据进行归一化

优点

减少对超参数的依赖，某些情况下可以取消Dropout方法或者L2正则项参数
减少对学习率的要求（加强对学习率参数的鲁棒性）
破坏原来的数据分布，一定程度上缓解过拟合，防止每批训练中某一个样本经常被选中
减少梯度消失（数据分布奇怪使激活函数输入接近0或者1，梯度很小）

算法流程

$x_{i}$是上一层的输出结果，B和Y是学习参数

计算上一层输出数据的均值

$\mu _{\beta}=\frac{1}{m} \sum_{i=1}^{m}\left ( x_{i} \right)$

计算上一层输出数据的标准差 $\sigma_{\beta}^{2}=\frac{1}{m} \sum_{i=1}^{m}(x_{i}-\mu _{\beta})^{2}$

进行归一化处理，得到
$x_{i}=\frac{x_{i}+\mu _{\beta}}{\sqrt{\sigma_{\beta}^{2}+\epsilon}}$

分母加一个极小值防止除0
重构
$y_{i}=\gamma \hat{x_{i}}+\beta$

gamma和beta是可学习参数。此时的均值是计算所有批次的mu_{beta}值的平均值得到的，标准差是每个批次的标准差的无偏估计。

和组归一化比较（Group Normalization）

如果batch比较小，导致估计的值和整个数据集的真实均值方差差距较大，BN的误差就会很大。

GN是将通道（channel）分成组，在每组内计算归一化的均值和方差，其准确度在各种批量大小下都很稳定

和权重归一化比较（weight normalization）

WN是对网络权重W进行归一化，适用于RNN，因为RNN处理的队列是变长的，基于时间状态计算，很难保存每个状态下的均值和方差，效率很低。

适用范围

适用于batch较大，数据分布比较接近的场景，不适用于动态网络和RNN结构。

允许较大的学习率
减弱对初始化的强依赖性，降低权重初始化的困难
保持隐藏层中数值的均值，方差不变，控制数据的分布范围，避免梯度消失和梯度爆炸
BN可以起到和dropout一样的正则化效果，在正则化方面，一般全连接层用dropout,卷积层拥BN
缓解内部协变量偏移问题，增加训练速度

BN存在的问题

每次是在一个batch上计算均值、方差，如果batch size太小，则计算的均值、方差不足以代表整个数据分布。
batch size太大：会超过内存容量；需要跑更多的epoch，导致总训练时间变长；会直接固定梯度下降的方向，导致很难更新。

梯度方向推导

背诵版本：

训练和测试时的区别：

常用的归一化层

BN代码实现，以及多卡训练的sync_bn

用numpy实现BN：

import numpy as np
from module import Layers

class BatchNormlization(Layers):
    """
    https://blog.csdn.net/weixin_44754861/article/details/108343938?utm_medium=distribute.pc_relevant.none-task-blog-2~default~baidujs_utm_term~default-5.pc_relevant_paycolumn_v3&spm=1001.2101.3001.4242.4&utm_relevant_index=7

    """
    def __init__(self, name, x,eps =1e-7, momentum =0.9, mode = "train"):
        super(BatchNormlization).__init__(name)
        self.eps =eps
        self.input = x
        n, c, h, w = x.shape
        self.momentum = momentum
        # 相同batch里不同样本的相同的通道来计算均值和方差
        self.running_mean = np.zeros(c)
        self.running_var = np.zeros(c)
        self.gamma = np.random(c)
        self.beta =np.random(c)
        self.mode = mode

    def add_dim(x, dim):
        return np.expand_dims(x, axis=dim) # batch 

    def forward(self):
        ib, ic, ih, iw = self.input.shape

        self.input = self.input.transpose(1, 0, 2, 3).reshape([ic, -1]) # n,c,h,w ->c, n*h*w
        if self.mode =="train":
            self.var = np.sqrt(self.var +self.eps) # 
            self.mean = np.mean(self.input, axis=0) # 每个channel的均值
            self.mean = self.add_dim(self.mean, 1) # 与后面的self.input 维度一致
            self.var = np.var(self.input, axis=0) #每个channel的方差
            self.var = self.add_dim(self.var , 1)
            self.gamma = self.add_dim(self.gamma, 1)
            self.beta = self.add_dim(self.beta, 1)
            self.running_mean = self.momentum * self.running_mean + (1-self.momentum) *self.mean
            self.running_var = self.momentum * self.running_var + (1-self.momentum) *self.var
            self.input_ = (self.input -  self.running_mean)/(self.running_var + self.eps)
            dout = (self.input_*self.gamma +self.beta ).reshape(ic,ib, ih, iw).transpose(1, 0, 2, 3)
            self.cache = (self.input_, self.gamma, (self.input - self.running_mean, self.running_var + self.eps))
        elif self.mode =="test":
            x_hat = (self.input - self.running_mean) / (np.sqrt(self.running_var + self.eps))
            dout = self.gamma * x_hat + self.beta
        else:
            raise ValueError("Invalid forward batch normlization mode")
        return dout, self.cache


    def backward(self, dout):
        N, D = dout.shape
        x_, gamma, x_minus_mean, var_plus_eps =self.cache

        # calculate gradients
        dgamma = np.sum(x_ * dout, axis=0)
        dbeta = np.sum(dout, axis=0)

        dx_ = np.matmul(np.ones((N,1)), gamma.reshape((1, -1))) * dout
        dx = N * dx_ - np.sum(dx_, axis=0) - x_ * np.sum(dx_ * x_, axis=0)
        dx *= (1.0/N) / np.sqrt(var_plus_eps)

        return dx, dgamma, dbeta

    def update(self, lr, dgamma, dbeta):
        self.gamma -= dgamma *lr
        self.beta -= dbeta*lr

BN 的性能和 batch size 有很大的关系。batch size 越大，BN 的统计量也会越准。然而像检测这样的任务，占用显存较高，一张显卡往往只能拿较少的图片（比如 2 张）来训练，这就导致 BN 的表现变差。一个解决方式是 SyncBN：所有卡共享同一个 BN，得到全局的统计量。

PyTorch 源码解读之 BN & SyncBN：BN 与多卡同步 BN 详解

单卡上的 BN 会计算该卡对应输入的均值、方差，然后做 Normalize；SyncBN 则需要得到全局的统计量，也就是“所有卡上的输入”对应的均值、方差。一个简单的想法是分两个步骤：

每张卡单独计算其均值，然后做一次同步，得到全局均值
用全局均值去算每张卡对应的方差，然后做一次同步，得到全局方差

但两次同步会消耗更多时间，事实上一次同步就可以实现

Layer Normalization

LN为了解决什么问题？

如果一个神经元的输入分布在神经网络中是动态变化的，比如循环神经网络（RNN），那么无法应用BN操作。因此，针对BN不适用于深度不固定的网络（RNN，sequeece长度不一致）的问题，LN针对单个训练样本进行归一化操作，即对每一个样本中多个通道（channel）进行归一化操作。

LN针对单个样本进行归一化操作。具体来说，对于输入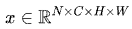,LN对每个样本的C、H、W维度上的数据求均值和方差，保留N维度。LN中不同的输入样本有不同的均值和方差。

$\mu_n(x)=\frac{1}{CHW}\sum_{c=1}^{C}\sum_{h=1}^{H}\sum_{w=1}^{W}x_{nchw}$

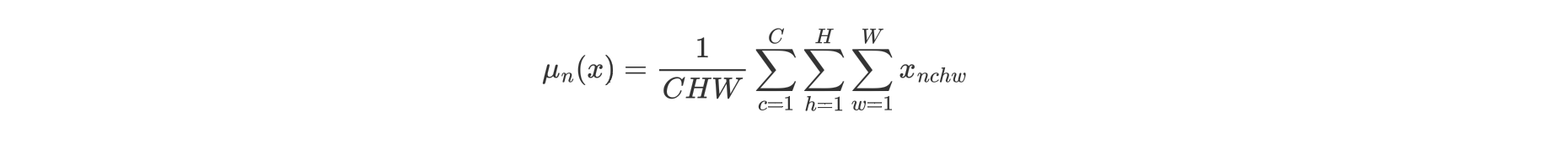
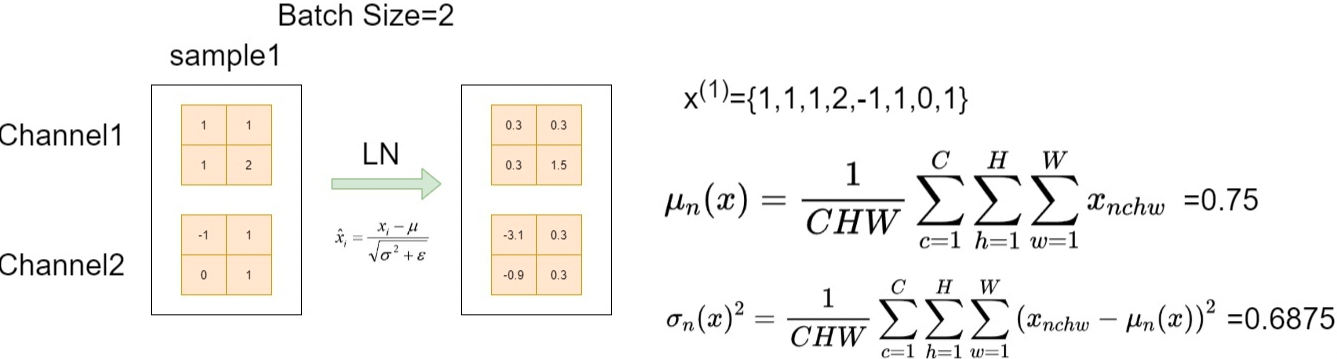
LN的优势

不需要批训练，在单条数据内部机就能归一化。不依赖batch_size和输入sequence的长度，因此可以用于batch size为1和RNN中。LN用于RNN效果比较明显，但是在CNN上，效果不如BN。

import torch
import torch.nn as nn
import numpy as np

# feature1 = np.array([[[0, 1], [1, -1]], [[-1, 0], [0, 2]]])
# feature2 = np.array([[[1, 0], [3, 1]], [[0, 1], [4, -1]]])
"""
    Examples::
        >>> input = torch.randn(20, 5, 10, 10)
        >>> # With Learnable Parameters
        >>> m = nn.LayerNorm(input.size()[1:])
        >>> # Without Learnable Parameters
        >>> m = nn.LayerNorm(input.size()[1:], elementwise_affine=False)
        >>> # Normalize over last two dimensions
        >>> m = nn.LayerNorm([10, 10])
        >>> # Normalize over last dimension of size 10
        >>> m = nn.LayerNorm(10)
        >>> # Activating the module
        >>> output = m(input)
"""
sample1 = torch.tensor([[[1, 1], [1, 2]], [[-1, 1], [0, 1]]],dtype=torch.float32)
sample2 = torch.tensor([[[0, -1], [2, 2]], [[0, -1], [3, 1]]],dtype=torch.float32)
ln = nn.LayerNorm([2,2,2],elementwise_affine=False)
output1 = ln(sample1)
output2 = ln(sample2)
print(output1)
# print(output2)

mean = np.mean(sample1.numpy())
var = np.var(sample1.numpy())
output3 = (sample1.numpy()-mean)/np.sqrt(var+1e-5)
print(mean)
print(var)
print(output3)

Upperlan

深度学习基础-关于Normalization的各种